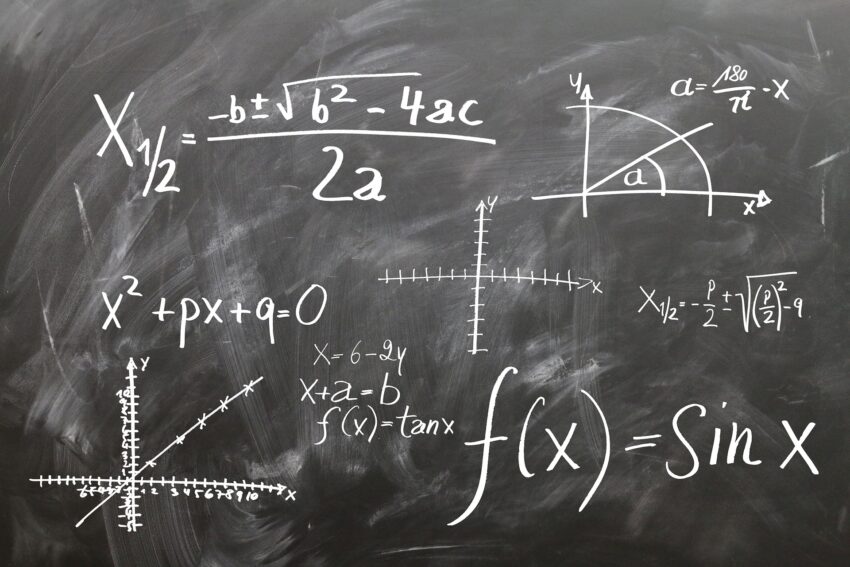POLİNOMLAR

a₀,a₁,a₂,a₃ …, a_n ϵ R ve n ϵ N olmak üzere P(x) = a₀+a₁.x+a₂.x²+a₃.x³+….+a_n.xⁿ biçimindeki  ifadelere x değişkenine göre düzenlenmiş reel katsayılı polinom (çok terimli) denir.

Burada a₀, a₁, a₂, a₃ …, a_n reel sayılarına polinomun katsayıları, a₀, a₁.x, a₂.x², a₃.x³,…., a_n.xⁿ ifadelerine polinomun terimleri olarak adlandırılır.

a_n.xⁿ  terimindeki a_n sayısına terimin katsayısı, x’in kuvveti olan n sayısına terimin derecesi olarak adlandırılır.

Derecesi en büyük olan terimin derecesine polinomun derecesi denir ve der [P(x)] ile gösterilir. Derecesi en büyük olan terimin katsayısı ise polinomun baş katsayısı olarak adlandırılır.

Polinomlar katsayılarına göre isimlendirilir. Katsayılarımız reel sayı ise reel katsayılı polinomlar, rasyonel sayı ise rasyonel katsayılı polinomlar, tam sayı ise tam katsayılı polinom denir.

Örnek 1:   P(x) = 8x³ – 3x² + 4x – 9

1. a) P(x) polinomunun katsayılarını yazınız:
2. b) P(x) polinomunun terimlerini yazınız:
3. c) P(x) polinomunun baş katsayısını yazınız:
4. d) P(x) polinomunun derecesini yazınız:

Çözüm 1:

1. a) 8,-3,4,-9
2. b) 8x³ ,– 3x² , 4x ,- 9
3. c) 5
4. d) der [P(x)] = 3

Örnek 2: 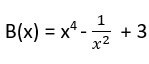 ifadesi bir polinom mudur? Değil ise sebebiyle birlikte açıklayınız?

Çözüm 2:
B(x) ifadesi bir polinom değildir çünkü  -1/ x² = – x^-2 teriminin kuvveti -2 N dir. Değişkeninin kuvvetleri (üsleri) doğal sayı olan fonksiyonlara polinom denir.

Sabit Polinom

c ϵ R ve c≠0 ( c, 0 dan farklı bir reel sayı ) olmak üzere P(x) = c biçimindeki polinomlar sabit polinom olarak adlandırılır. Sabit polinomun derecesi  0 dır.

Sıfır Polinomu

P(x) = 0 biçimindeki polinomu sıfır polinomu olarak adlandırılır. Sıfır polinomunun derecesi tanımsızdır.

Örnek 3: P(x) = (2a–3).x² + b.x + 2.x + 5 ifadesi sabit polinom olduğuna göre a.b çarpımının değerini bulunuz.

Çözüm 3:
Verilen ifadenin sabit polinom olması için değişkenin olmaması gerekir. Bu sebeple değişkenin katsayısı 0 olmalıdır.

2.a – 3 = 0        ,           x.(b + 2) = 0
2.a = 3                             b + 2 = 0
a = 3/2                             b = – 2
Buradan  a.b =  – 2 = – 3

Polinomların Eşitliği

Aynı dereceli terimlerinin katsayıları eşit olan polinomlar eşittir.

Örnek 4:
P(x) = ax² + (b – 3)x + 5
Q(x) = – 3x²  + 5x + c + 7

P(x) = Q(x) olduğuna göre a,b,c nin alabileceği değeri bulunuz.

Çözüm 4:
P(x) = Q(x) ise  ax² + (b – 3)x + 5 = – 3x²  + 5x + c + 7

• a = – 3
• b – 3 = 5
• b = 8
• c + 7 = 5
• c = – 2

Örnek 4:

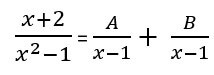
olduğuna göre A ve B nin değerini bulunuz.

Çözüm 4:

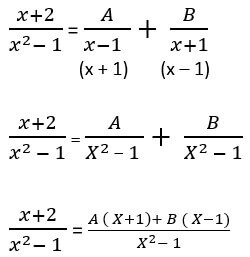X + 2 = Ax + A + Bx – B
X + 2 = x.(A+ B) + A – B

• A + B = 1
• A – B = 2
• 2A = 3
• A = , B =

Polinomlarda İşlemler

1) Toplama İşlemi

İki polinom toplanırken; dereceleri aynı olan terimlerin katsayıları kendi aralarında toplanır, o terimin kat sayısı olarak yazılır.

• xⁿ + b. xⁿ = (a + b). xⁿ
• xⁿ + b.xⁿ = (1+b) . xⁿ

2) Çıkarma İşlemi

İki polinom çıkarılırken; dereceleri aynı olan terimlerin katsayıları kendi aralarında çıkarılır, o terimin katsayısı olarak yazılır.

3) Çarpma İşlemi

İki polinomun çarpımı; birisinin her teriminin diğerinin her bir terimi ile ayrı ayrı çarpımlarından elde edilen terimlerin toplamına eşittir.

• axⁿ . bx^m = a.b.x^m+n
• xⁿ . bxⁿ = b.x^n+m

4) Bölme İşlemi

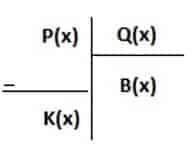P(x) : Bölünen
Q(x) : Bölen
B(x) : Bölüm
K(x) : Kalan

Olmak üzere bölme işleminde

1. der [ P(x) ] ≥ der [ Q(x)]
2. der [K(x) ] < der [ Q(x) ]
3. P(x) = Q(x) . B(x) + K(x)
4. der [ K(x) ] < der [B (x) ] ise Q (x ) ile B(x) in yer değiştirmesi kalanı değiştirmez.
5. K (x) = 0 ise P(x) polinomu  Q(x) polinomuna tm olarak bölünür. Bu durumda  P(x) in çarpanlarından biri Q(x) polinomudur.

Polinomlarda Bölme İşleminin Yapılışı

Polinomlarda bölme işlemi sayılarda bölme işlemine benzer şekilde yapılır. Bunun için sırasıyla aşağıdaki işlemler yapılır.

1. Bölünen ve bölen polinomlar x değişkeninin azalan kuvvetlerine göre sıralanır.
2. Bölünen polinomun soldan ilk terimi , bölen polinomun soldan ilk terimine bölünür. Çıkan sonuç bölümün ilk terimi olur.
3. Bulunan bu sonuç bölen polinomun bütün terimleri ile çarpılarak aynı dereceli terimler alt alta gelecek şekilde bölünen polinomun altına yazılır.
4. Bölünenin altına yazılan çarpım polinomu , bölünenin polinomdan çıkarılır.
5. Yukarıdaki işlemlere , kalan polinomun derecesi , bölen polinomun derecesinden küçük oluncaya kadar devam eder.

Kural

P(x)’ in Q(x) ile bölümünden elde edilen bölümün polinomu B(x) olsun.

der [P(x)]=m ve der[Q(x)] = n
m>n olmak üzere

• der [P(x) + Q(x) ] = m
• der [P(x) – Q(x) ] = m
• der [ P(x) . Q(x) ] = m + n
• der [ B(x) ] = m – n
• der [ = k.der [P(x)] = k.m dir.

P(x)‘ in x = k için Değeri
P(x) = a₀+a₁.x+a₂.x²+a₃.x³+….+a_n.xⁿ   polinomunun x=k için değeri
P(k) = a₀+a₁.k+a₂.k²+a₃.k³+….+a_n.kⁿ

Kural

P(x) = a₀+a₁.x+a₂.x²+a₃.x³+….+a_n.xⁿ    polinomunda x=1 yazılırsa

P(1) = a₀+a₁+a₂+a₃+….+a_n  olur.

• Bu durumda  P(1) in değeri  P(x) polinomunun katsayılar toplamıdır.
• Bir polinomda x yerine 1 yazılırsa, o polinomun katsayılar toplamı bulunur.

Kural

P(x)=a₀+a₁.x+a₂.x²+a₃.x³+….+a_n.xⁿ   polinomunda  x=0 yazılırsa,
P(0)=a₀  olur.

• Bu durumda  P(0)‘ın değeri  P(x) polinomunun sabit terimidir.
• Bir polinomda x yerine 0 yazılırsa, o polinomun sabit ( x’ten bağımsız ) terim bulunur.

P(x)‘ in ax + b ile Bölünmesiyle Elde Edilen Kalan

P(x) = (ax + b).B(x)+K
ax+b=0 ise x =-b/a
P(-b/a) = (a.(-b/a)+b).B(-b/a)+ K= K

Yani P(x) polinomunun ax+b ile bölünmesiyle elde edilen kalanı bulmak için ax+b= 0 denkleminin kökü olan x=-b/a için P(x) polinomunun değeri olan P(-b/a) hesaplanır.

Sonuç

• P(x) polinomunun x – a ile bölümünden kalan  P(a)
• P(x + b) polinomunun x – a ile bölümünden kalan P(a + b)
• P(3x + b) polinomunun x – a ile bölümünden kalan P(3a + b) dir.

P(x)’in x^n + a İle Bölümünden Kalan

Derecesi n’den büyük olan bir polinomun xⁿ+ a ile bölümünden kalanı bulmak için, yerine –a yazılır.

(xⁿ+a=0 ise xⁿ=-a)

P(x) ‘ in (x – a) . (x – b) Çarpımı İle Bölünmesi

1. P(x) polinomu (x – a).(x – b) çarpımı ile tam olarak bölünebiliyorsa x–a ve x–b çarpanlarına ayrı ayrı bölünebilir.
2. x–a ve x–b aralarında asal polinomlar olmak üzere; P(x) bu polinomlara ayrı ayrı tam olarak bölünebiliyorsa, (x–a).(x–b) çarpımı ile de tam olarak bölünür.

P(x)‘ in ( ax + b )² İle Bölünebilmesi

P(x) polinomu (ax+b)² ile tam olarak bölünebiliyorsa, P(x) polinomu ve P’(x) polinomu ax+b ye tam olarak bölünür. (P’(x), P(x) polinomunun türevidir.)

Bu durumda P(x) polinomu (ax+b)² ile tam olarak bölünüyorsa P(-b/a)= 0 ve P’(-b/a) = 0 olur.