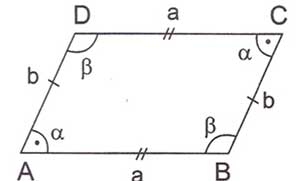
Karşılıklı kenarları birbirine paralel ve eş olan dörtgenlere paralelkenar denir.
[AB][AB]//[CD][CD]
[BC][BC]//[AD][AD]
Paralelkenar Özellikleri:
1. Paralelkenarın karşılıklı açıları birbirine eşittir.
∝+β=180
2. Paralelkenarın karşılıklı kenarları birbirine eşittir.
|BC|=|AD||BC|=|AD|=b
3. Paralelkenarın köşegenleri birbirini ortalar.
|AO|=|CO||AO|=|CO|
|BO|=|DO||BO|=|DO|
Yani bölünen köşegenin her iki parçası birbirine eşittir.
4. [AE][AE] ile [BE][BE] açıortay ise m(ˆAEBAEB^)=900900
Açıortayların kesiştikleri bölümdeki açı 900900’dir.
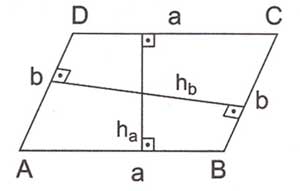
Paralelkenarın Alanı
Alan (ABCD)=a.haha=b.hbhb
Kenar ve o kenarın yüksekliğinin çarpımı paralelkenarın alanını vermektedir.
a.
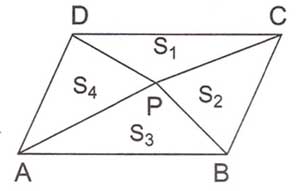
S1S1=S2S2=S3S3=S4S4
Köşegenlerle 4’e ayrılmış bir paralel kenarın her bir bölümünün alanı birbirine eşittir.
b. “P”, paralel kenar içinde herhangi bir nokta olsun.
S1S1+S3S3=S2S2+S4S4=A(ABCD)2A(ABCD)2
Oluşan üçgenlerden karşılıklı olanlarının alanları toplamı paralelkenar alanının yarısına eşittir.
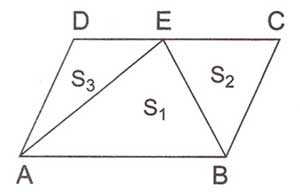
S1S1=S2S2+S3S3 ve Alan (AEB)= A(ABCD)2A(ABCD)2
Paralel kenar bir kenardan belirlenen herhangi bir tepe noktasından bölünerek üç tane üçgen elde edilir. Şekilde görüldüğü gibi büyük üçgenin alanı diğer iki küçük üçgenin alanlarının toplamına eşittir.